Using Jax to Compute Block-Low-Rank Format Preconditioners on Graphics Cards

The Block-Low-Rank (BLR) representation of a matrix $A$ is a data-sparse representation of $A$ which uses low-rank factors to represent off-diagonal blocks and small dense matrices to represent its diagonal blocks. This format is useful in sparse linear algebra because it can approximate an inverse or a factor which is dense but has compressible off-diagonal blocks. Unfortunately the BLR format is unwieldy to code efficiently and harder on top of that to approximate a given matrix $A$ in this format (in spite of randomized algorithms that already exist which I will comment on later). In this blog post I convert core BLR operations (like matrix-vector product) to tensor contraction which allows a concise implementation in the jax python library. Jax converts the tensor contractions to XLA for efficient evaluation on graphics cards. A side benefit of the JAX translation is access to algorithmic differentiation and thus we also achieve a relatively simple way to compute BLR via a stochastic-gradient-descent-like algorithm. I show here the translation to tensor contraction, JAX implementation, and preconditioner results for GMRES(1) using the subsequently learned BLR representations of the inverse $A^{-1}$. I start with the preconditioner formulation.

Motivation for using BLR as a Preconditioner

Suppose we have an $m \times m $ sparse matrix $A$ and wish to solve the system of linear equations

Since $A$ is sparse the common solution is an iterative solver, but iterative solvers generally require a preconditioner for robust and efficient convergence. For the purpose of this blog post we will consider a preconditioner $P$ as an approximation to the inverse of $ A $:

A well-known fact about sparse matrices possessing the strong hall property is that absent special numerical cancellation, the structural inverse of such a matrix is dense. Since sparse matrices tend to have extremely large dimensions $m$, this means a preconditioner $P$ has the task of approximating $m^2$ numbers, which is an impossible task for large $m$.

The BLR format compresses an otherwise intractably huge dense matrix by assuming its off-diagonal blocks have low rank. I illustrate with a $ 4 \times 4 $ block matrix below

$$ P \approx \begin{pmatrix} D _ 1 + U_{1,1}V_{1,1}^T & U_{1,2}V_{1,2}^T & U_{1,3}V_{1,3}^T & U_{1,4}V_{1,4}^T \\ U_{2,1}V_{2,1}^T & D _ 2 + U_{2,2}V_{2,2}^T & U_{2,3}V_{2,3}^T & U_{2,4}V_{2,4}^T \\ U_{3,1}V_{3,1}^T & U_{3,2}V_{3,2}^T & D _ 3 + U_{3,3}V_{3,3}^T & U_{3,4}V_{3,4}^T \\ U_{4,1}V_{4,1}^T & U_{4,2}V_{4,2}^T & U_{4,3}V_{4,3}^T & D _ 4 + U_{4,4}V_{4,4}^T \end{pmatrix} $$

The matrices $U_{i,j},V_{i,j}$ are generally tall skinny matrices representing a low-rank factorization of their corresponding block. The implementation below permits a low-rank correction on diagonal blocks as well as the dense $D_i$ term. By storing $U,V$ instead of their represented dense matrices we achieve considerable space and computational savings.

I will show later how to compute $U_{i,j},V_{i,j},D _ i$, but first I show how to compute matrix-vector products with this format efficiently. The matrix-vector operation is necessary for preconditioners and this unfortunately proves challenging to implement for the BLR format, particularly on GPUs, because it results in a significant number of small dense matrix algebra operations which must be carefully batched and fused for efficiency on modern CPUs and GPUs as well. Fortunately the Jax library can automate a lot of this for us provided we can write the algorithm under its strict limitations. I will show how to do this next.

Implementing BLR Matrix-Vector Product as Tensor Contraction

Since for each $i,j$, $U_{i,j},V_{i,j}$ are matrices, $U,V$ are four-dimensional tensors. We may also represent an $m \times 1 $ vector $ x $ as a $m _ b \times b $ 2-dimensional tensor.

Using einstein notation we can represent the matrix-vector product $Px$ using jax.lax.dot_general to compute tensor contractions as follows:

import jax
from jax import grad, jit, vmap
import jax.numpy as jnp
from functools import partial

@partial(jit, static_argnums=[1,2])
def eval_blr(blocks,m,blocksize,x):
    m,ncols=x.shape
    nblocks=m//blocksize
    Us,Vs,Ds=blocks
    xr = x.reshape((nblocks,blocksize,ncols))
    out=[]
    for i in range(0,nblocks):
        Vx = jax.lax.dot_general(Vs[i],xr,dimension_numbers=(
            ((2,), (1,)),
            ((0,), (0,))
            ))
        UVx = jax.lax.dot_general(Us[i],Vx,dimension_numbers=(
            ((0,2,), (0,1)),
            ((), ())
            ))
        out.append(UVx)
    y=jnp.asarray(out).reshape((nblocks,blocksize,ncols))
    z=y+jax.lax.dot_general(Ds,xr,dimension_numbers=(
            ((2,), (1,)),
            ((0,), (0,))
            ))
    return z.reshape((m,ncols))

Jax is able to offload these computations to a GPU which is very useful for general speedups, but on top of this it can compute the gradient for learning the parameters $ U,V,D $ which I show how to do next

Learning the BLR parameters

NOTE: Check the appendix section where I will give a list of approaches which did not work. As I wrote this blog post I ran results in parallel and I would find out later that the resulting preconditioners often were no better than a standard block-Jacobi preconditioner. Weeks later I found a viable approach which delivers a preconditioner consistently better than block Jacobi. I share this successful strategy here and give a rough summary of unsuccessful strategies in the appendix.

We can compute the parameters $ U,V,D $ through randomized algorithms (which I have linked below). As with any fixed-rank representation, these methods cannot produce a good approximation if the target inverse is not well represented by the chosen BLR block structure and ranks. This is a limitation of the representation as much as of the fitting algorithm.

An alternative approach which I take here is not to proceed in stages but to learn $U,V,D$ simultaneously through a stochastic-gradient-descent-like algorithm. The choice of objective function to minimize by the gradient-descent algorithm is motivated by the principle of convergence for Krylov methods which suggests that eigenvalue clustering in normal operators results in faster convergence (and therefore a preconditioner which can achieve this clustering should deliver fast convergence in a Krylov method).

Computing eigenvalues of the whole operator is too slow to use in an optimization method, and furthermore would require far too much memory for bigger matrices if approached through a dense eigendecomposition. Instead I use the fact that the Arnoldi factorization builds up an approximation to the spectrum of the matrix $ A \in \mathbb{R}^{m\times m} $ through

where $V_{k+1} \in \mathbb{R} ^ {m \times (k+1) } $ has orthonormal columns and $ \bar H_k \in \mathbb{R} ^ {(k+1) \times k} $ is upper Hessenberg. The eigenvalues of the leading $ k \times k $ square part are Ritz values which may approximate parts of the spectrum. If the final subdiagonal is zero, Arnoldi has found an invariant Krylov subspace for this starting vector. That event is not equivalent to globally clustered eigenvalues and can occur, for example, when the starting vector lies in a low-dimensional invariant subspace.

Or in words: find BLR parameters $U,V,D$ such that when we apply the Arnoldi factorization to the preconditioned operator $AM$ the residual norms at each step are as small as possible (if they are zero it signifies breakdown of the Arnoldi method, but this is very unlikely to be achieved exactly in the optimization process).

There are two important degeneracies in this raw objective. Scaling $M$ toward zero shrinks the Arnoldi subdiagonals without making $M$ a useful inverse, and using one starting vector can overfit the objective to that vector. A better version should control the scale and train over several starting vectors.

#From "Templates for the solution of linear algebraic eigenvalue problems" pg. 167 (ch7 algorithm 7.6)
@partial(jit, static_argnums=[0,2])
def arnoldi_dgks(A,v,k):
    norm=jnp.linalg.norm
    dot=jnp.dot
    eta=1.0/jnp.sqrt(2.0)

    m=len(v)
    V=jnp.zeros((m,k+1))
    H=jnp.zeros((k+1,k))
    #V[:,0]=v/norm(v)
    V = V.at[:,0].set(v/norm(v))
    for j in range(0,k):
        w=A(V[:,j])
        h=V[:,0:j+1].T @ w
        f=w-V[:,0:j+1] @ h
        s = V[:,0:j+1].T @ f
        f = f - V[:,0:j+1] @ s
        h = h + s
        beta=norm(f)
        #H[j+1,j]=beta
        H = H.at[j+1,j].set(beta)
        #V[:,j+1]=f/beta
        #A production version must handle beta == 0 without dividing by zero.
        V = V.at[:,j+1].set(f.flatten()/beta)
    return V,H

@partial(jit, static_argnums=[1,2])
def loss(params,m,blocksize,A,b):
    #Just hardcode size of arnoldi factorization for now
    k=10
    m,ncols=b.shape
    assert(ncols==1)
    #Implement the preconditioned operator
    @jit
    def Ac(x):
        return A @ eval_blr(params,m,blocksize,x.reshape((m,ncols)))
    #Construct the factorization.
    #I do not need V here so I discard it.
    _,H=arnoldi_dgks(Ac,b.reshape((m,)),k)
    #Sum up the lower subdiagonal entries of H
    return sum(H[j+1,j] for j in range(H.shape[0]-1))

The initial condition for the optimization problem. I simply set it to be equivalent to the identity matrix

def make_blr_id(A,blocksize,d=1):
    key=random.PRNGKey(0)
    A=sp.lil_matrix(A)
    m,_=A.shape
    assert( m%blocksize==0 )
    blockVs=[]
    blockUs=[]
    Ds=[]
    for i in range(0,m,blocksize):
        Us=[]
        Vs=[]
        ki=min(i+blocksize,m)-i
        ids=list(range(i,i+ki))
        Ds.append(jnp.eye(len(ids)))
        for j in range(0,m,blocksize):
            kj=min(j+blocksize,m)-j
            Vs.append(jnp.zeros((d,kj)))
            Us.append(jnp.zeros((ki,d)))
        blockVs.append(jnp.asarray(Vs))
        blockUs.append(jnp.asarray(Us))

    return jnp.asarray(blockUs,dtype=np.float64),jnp.asarray(blockVs,dtype=np.float64),jnp.asarray(Ds,dtype=np.float64)

  for it in range(nepochs):
      if plot_eigs and it%10==0:
          minx=min(np.real(eigA))
          maxx=max(np.real(eigA))
          miny=min(np.imag(eigA))
          maxy=max(np.imag(eigA))
          plt.close()
          blrA = eval_blr(blr,m,blocksize,Afull)
          eigbA = la.eigvals(blrA)
          plt.scatter(np.real(eigbA),np.imag(eigbA))
          ax = plt.gca()
          ax.set_xlim([minx,maxx])
          ax.set_ylim([miny,maxy])
          istr=str(it).zfill(5)
          plt.title(f"Preconditioned spectrum at SGD iteration {it}")
          plt.xlabel("Real part")
          plt.ylabel("Imaginary part")
          plt.savefig(f"eigs/{istr}.png")


      start=time.time()
      g = grad(loss)(blr,m,blocksize,Aj,b)
      updates,opt_state = opt.update(g,opt_state)
      blr = optax.apply_updates(blr,updates)
      err=loss(blr,m,blocksize,Aj,b)

      stop=time.time()
      print(f"it = {it},     elapsed = {stop-start : .4f},    loss = {err : 4f},    ")
      if losses and err<min(losses):
          f=open("blr_best.dat","wb")
          pickle.dump(blr,f)

      losses.append(err)

Preconditioner Results of Learned BLR on GMRES

To see how well this functions as a preconditioner I compare it to standard block-jacobi using the same block size as the BLR preconditioner:

#For comparison purposes: block jacobi preconditioner
import scipy.sparse.linalg as spla
def make_block_precon(A,blocksize):
    A=sp.lil_matrix(A)
    m,_=A.shape
    blocks=[]
    for i in range(0,m,blocksize):
        beg=i
        end=min(i+blocksize,m)
        ids=list(range(beg,end))
        blocks.append(spla.inv(A[np.ix_(ids,ids)].tocsc()))
    return sp.block_diag(blocks)

#Make a random sparse-banded matrix 
#with bands in `bands`
#its diagonal shifted by `diag`
def make_banded_matrix(m,diag,bands,rng):
    subdiags=[rng.uniform(-1,1,m) for _ in bands] + [rng.uniform(0.1,1,m) + diag] + [rng.uniform(-1,1,m) for _ in bands]
    offs = [-x for x in bands] + [0] + [x for x in bands]
    return sp.diags(subdiags,offs,shape=(m,m))


#Example matrix
m=1024
seed=23498732
rng=np.random.default_rng(seed)
diag=3
A=make_banded_matrix(m,diag,[1,2,3,10,40,100],rng)

The diag parameter shifts the diagonal of A. Moving it toward zero tends to reduce diagonal dominance and made these sampled systems harder.

Early Results

I chose parameters m=512,blocksize=128 so that the experiments would be able to run on my laptop. I will later run larger experiments on GCP A100 instances.

First I compare preconditioner quality by measuring the residual norm at each GMRES iteration for both the BLR preconditioner and block-jacobi based on the same blocksize.

I also show how the SGD training loss looks like per iteration. It appears there is likely room for more improvement if I let the iterations proceed longer

Finally I show animations for what the right-preconditioned operator $AM$ spectrum looks like as the SGD iterations proceed. We can see a squeezing of the spectrum to a point - this is expected because we are driving the Arnoldi iterations toward a breakdown scenario for the chosen starting vector. Arnoldi often resolves exterior Ritz values early, but the animation computes the full small-problem spectrum; the observed motion should not be treated as a guarantee for larger matrices or other starting vectors.

`diag`	GMRES Iteration History
4.0
3.0
2.0
1.5
1.0

`diag`	Training Loss
4.0
3.0
2.0
1.5
1.0

`diag`	Spectrum GIF
4.0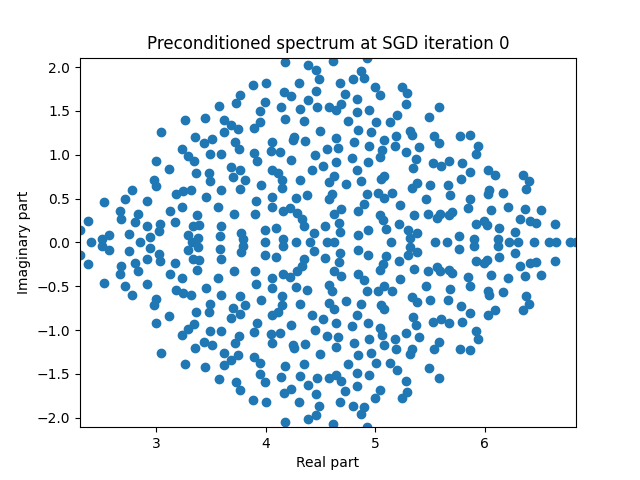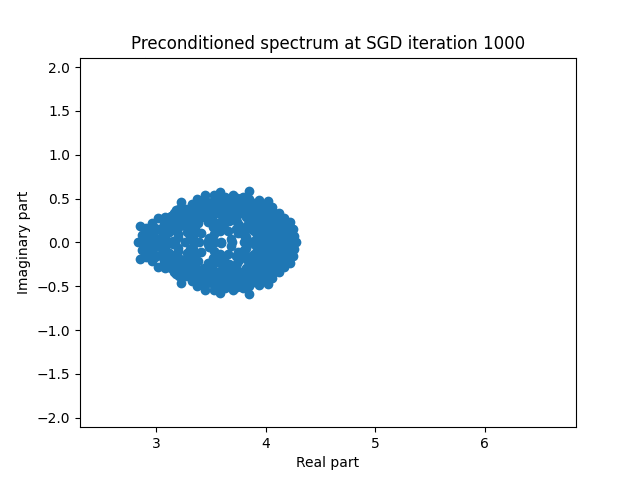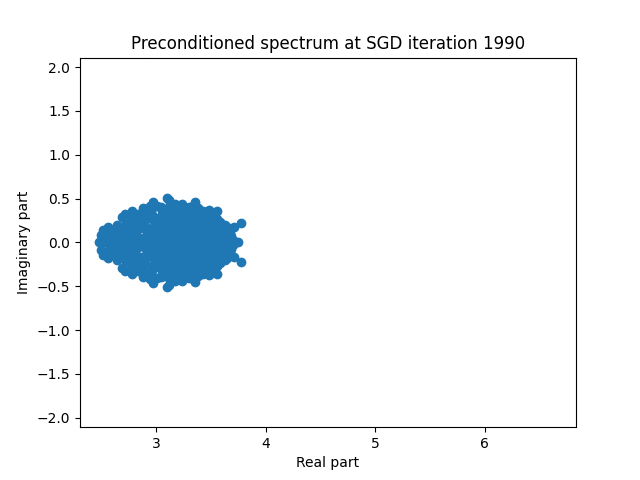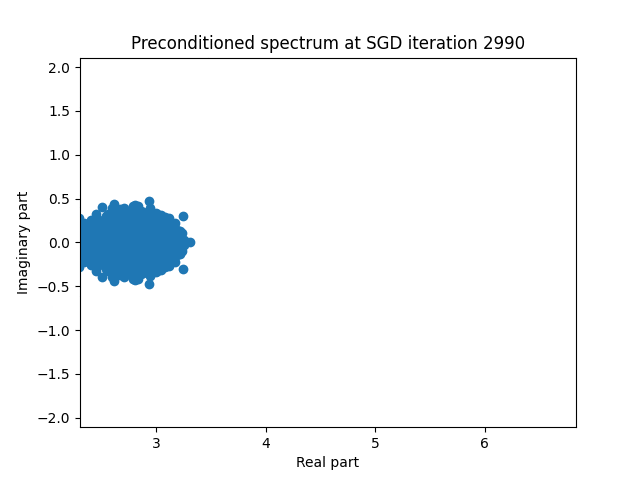
3.0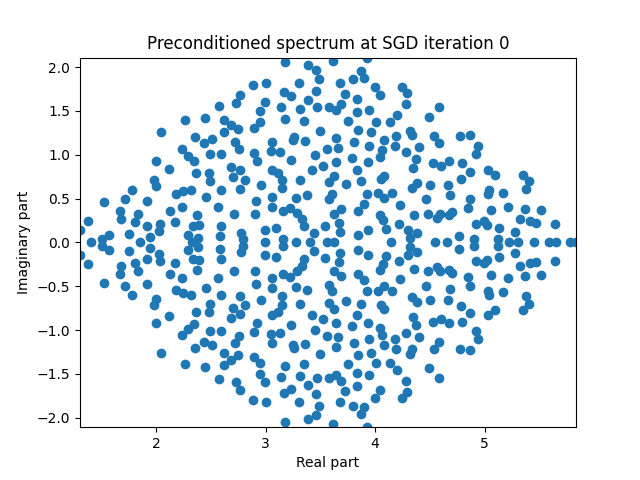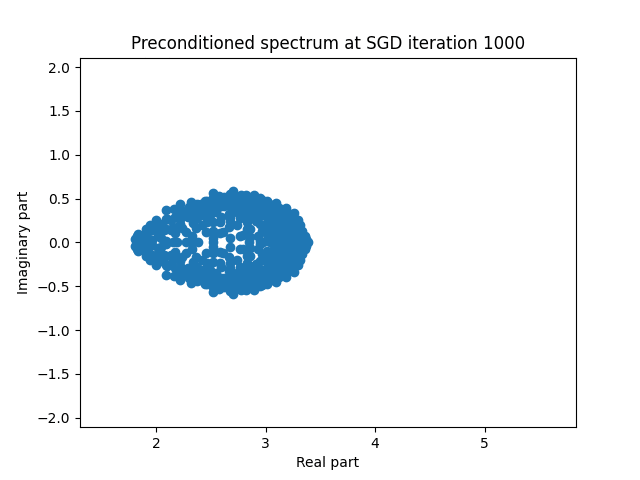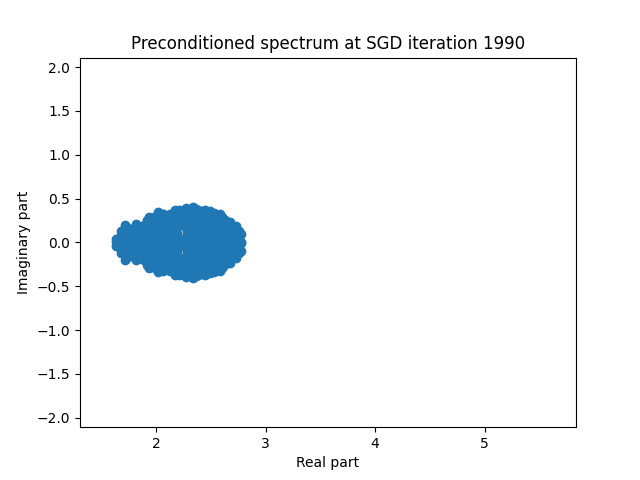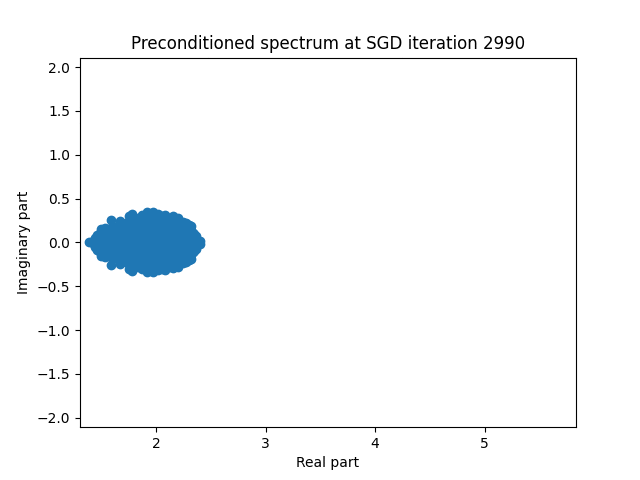
2.0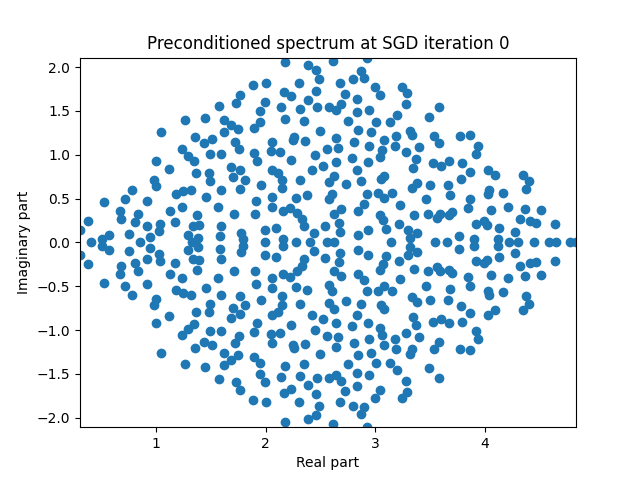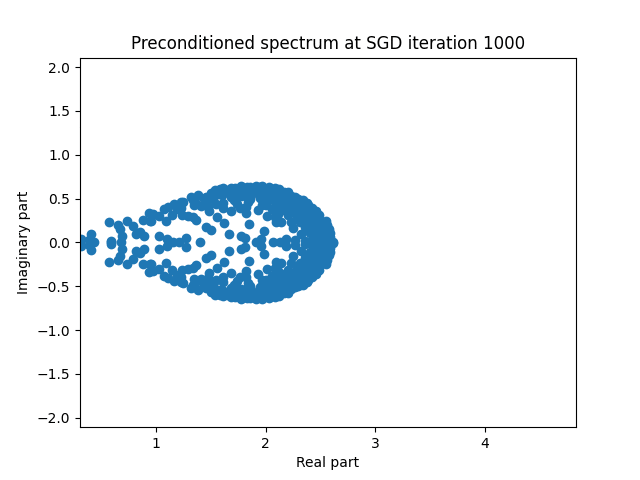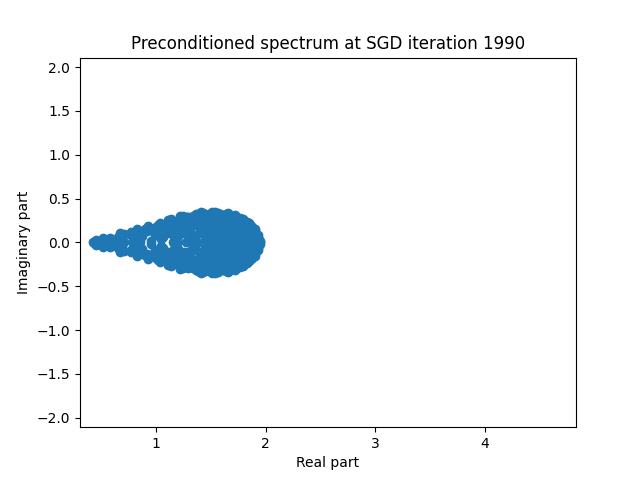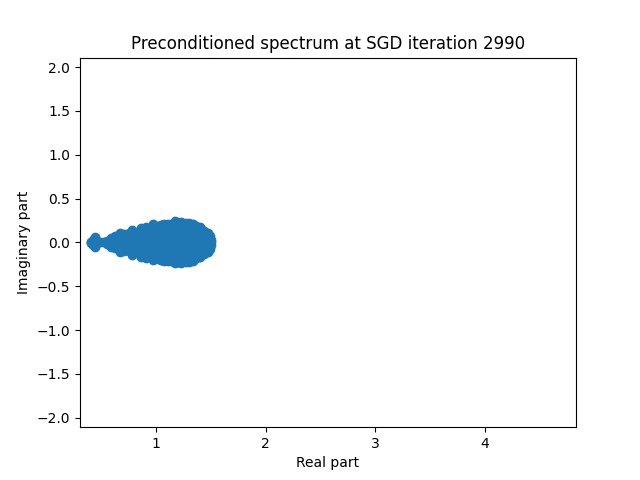
1.5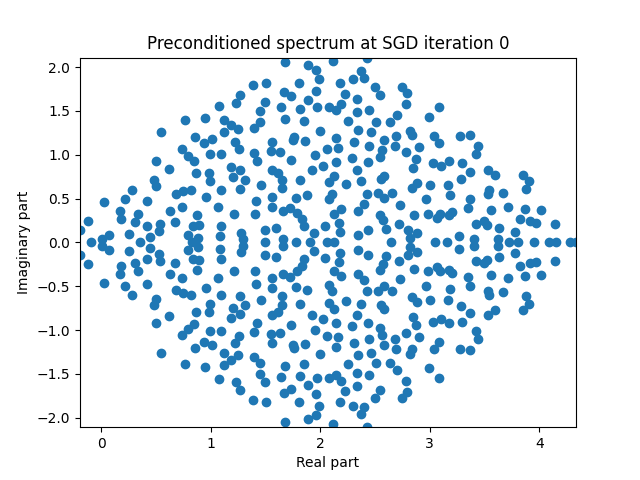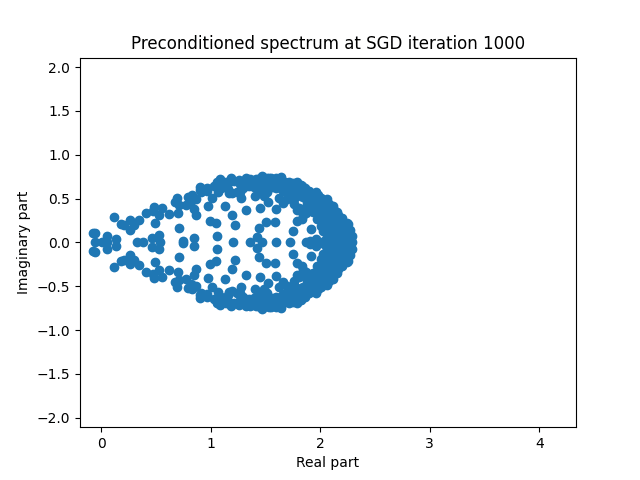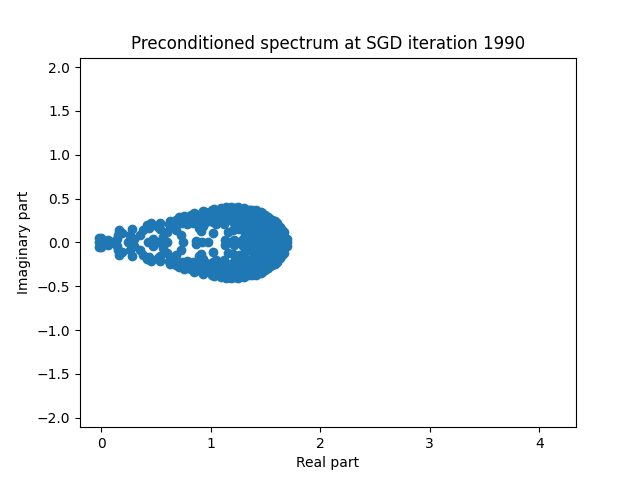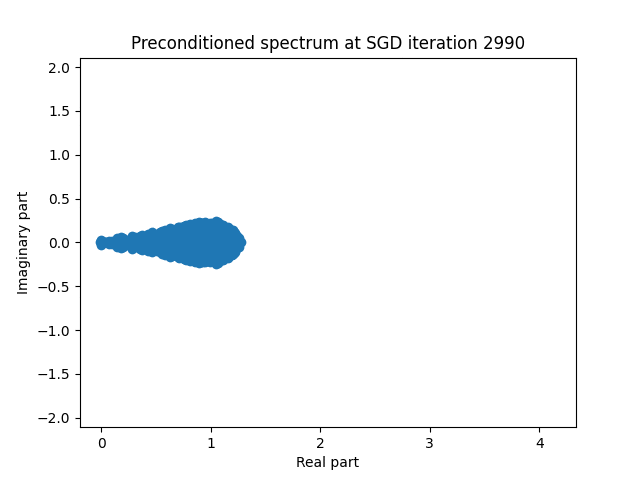
1.0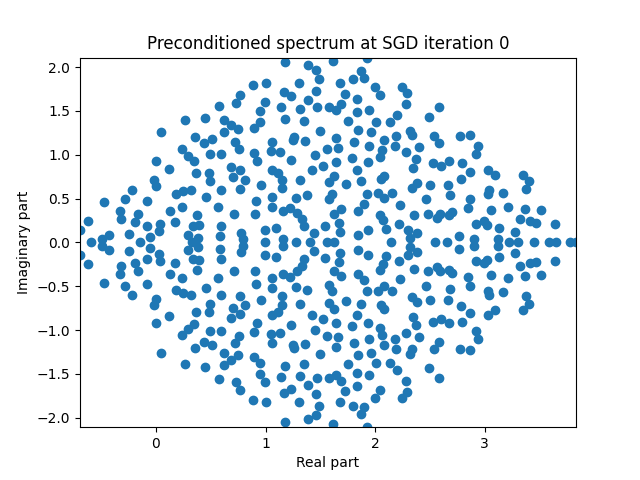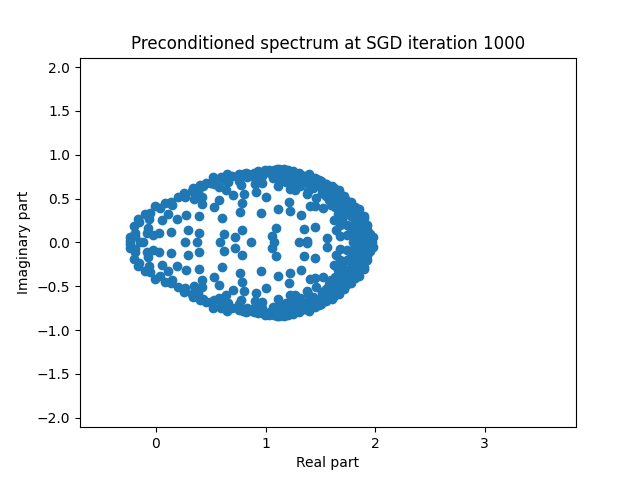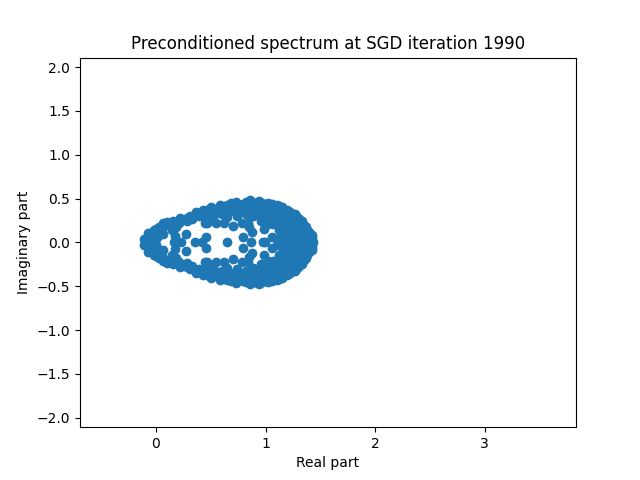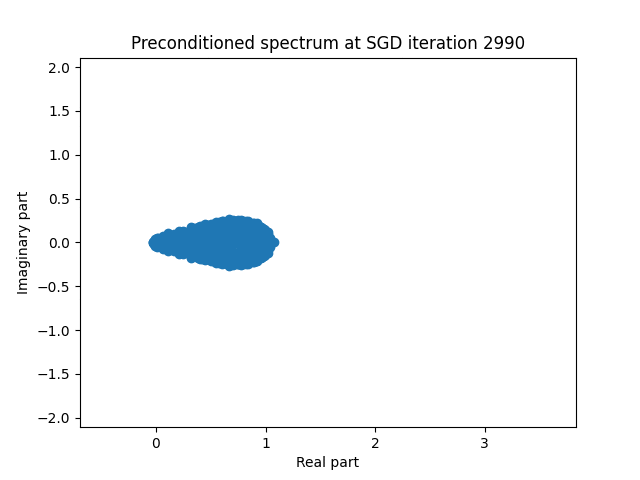

The learned BLR preconditioner worked best when we had diag>=2 which corresponded to definite operators. I believe if we had a simple preconditioner which dealt only with this part of the spectrum we could combine the result with the learned BLR preconditioner. One way we could possibly approach this would be to split $ A = \frac{1}{2}(A+A^T) + \frac{1}{2}(A-A^T)$ and compute a cholesky-like factorization for the symmetric part leaving the BLR factorization to the resulting shifted skew-symmetric system.

Conclusions

While I do not think I have made a very useful preconditioner algorithm through the SGD training procedure I do believe that the formulation of the BLR preconditioner as tensor contractions could prove very useful for experimenting with BLR preconditioners on the GPU. The SGD algorithm could perhaps be further improved for more rapid convergence as well though, and also could be used to “refine” an existing BLR preconditioner (achieved through, for example, a randomized algorithm). Any continuation should remove the scale degeneracy, use multiple starting vectors, and compare total training and application cost rather than iteration counts alone.

Appendices 1: References

Datasparse formats (not just BLR) has received significant interest after Martinsson published a randomized algorithm to approximate an input matrix with a datasparse representation, an algorithm that can readily be adapted for the BLR case. The Martinsson algorithm was very interesting because it was “black box”: you did not need to know the actual entries of $A$ to use it, only the ability to compute matrix-vector products $Ax$. This enabled a new class of preconditioners which have proven extremely powerful for a wide variety of problems. I give below a small list of references which form a good starting place for learning more about these preconditioners

Appendices 2: Failures

When I started this blog post I had several numerical experiments running for fairly large problems using GCP A100 instances. I found out mid-writing that these did not work very well. My choice of objective function at the beginning was not ideal for producing a good preconditioner for GMRES. Here is what I tried that did not seem to work:

I believe that these did not work because although they superficially improved commonly used metrics to determine preconditioner quality, they tended to increase nonnormality of the resulting operator $AM$ in equal measure. This resulted in a preconditioner that looks good “on paper” but does not work as expected in practice.

The final objective based on Arnoldi at least observes the action of the nonnormal operator $AM$, rather than using eigenvalues alone, though it retains the degeneracies described above.

\(m\)	Dimension of \(A\)
\(b\)	Block size
\(m _ b = m/b\)	Number of blocks
\(k\)	off-diagonal rank